Theory of computation

Compiler basics

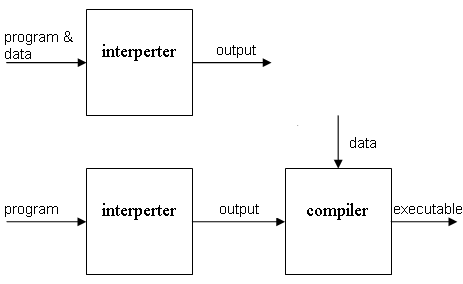
• Compilers vs interperters
  
  
  
  
• Structure of a compiler
  The structure of a compiler consists of 5 major fases:
  
  
  1. Lexical analysis
     Lexical analysis divides program text into words also known as lexemes by reading the text from left to right.
     
     The output of the lexical analysis is a series of tokens where the token class for each lexeme is identified. A token consists of: <token class, lexeme>
     
     Lookahead is always needed to decide where one token ends and the next token begins.
     Minimize the amount of lookaheads to simplify the implementation of the lexical analyzer.
     
     
  2. Parsing
     Parsing is diagramming sentences to understand sentence structure.
     
     
  3. Semantic Analysis
     Understand meaning to sentences to catch inconsistencies.
     
     
  4. Optimization
     Automatically modify program so that they run faster, use less memory, reduce power usage, use less database/network connection etc.
     Modern compilers spend large amount of time in optimization compare to other fases.
     
     
  5. Code generation
     Produces usually assembly code (translate into another language).
     
     
• Regular languages
  Regular languages are used to determine which set of strings is in a token class.
  
  To define regular languages, regular expressions are used. Each regular expression (=syntax) denotes a set of strings (=regular languages).
  There are two basic regular expressions:
  
  
  • A single character
    
    A single character 'c' is an expression which denotes a language containing a string with a single character:
    'c' = {"c"}
    
    
  • Epsilon
    
    ε is an expression which denotes a language containing an empty string:
    ε = {""}
    
    
  There are three compound regular expressions:
  
  
  • Union (∪)
    
    A + B is an expression which denotes a language containing a string:
    A + B = {a | a∈A} ∪ {b | b∈B}
    
    
  • Concatenation (∧)
    
    AB is an expression which denotes a language containing a string:
    AB = {ab | a∈A ∧ b | b∈B}
    
    
  • Iteration (*)
    
    A^* is an expression which denotes a language containing a string:
    A^* = ∪_i>=0Aⁱ
    Aⁱ = A₀, A₁, A₂, A₃,...
    A₀ = ε
    Note: The empty string (ε) is always a elements of A^*.
  
  Definition: The regular expression over Σ (=alphabet) are the smallest set of expressions including:
  R = ε | 'c' | R+R | RR | R^*
  Note: 'c' ∈ Σ
  
  If we want to know the regular language we need to know what the alphabet (Σ) is.
  
  Σ = {0,1}
  
  Question: The expression 1^* what language does it denotes?
  Answer: ε + 1 + 11 + 111 + 1111 + ...
  All strings of 1's.
  
  Question: The expression (1+0)1 what language does it denotes?
  Answer: {11,01}
  
  Question: The expression 0^* + 1^* what language does it denotes?
  Answer: {0ⁱ | i>=0} ∪ {1ⁱ | i>=0}
  
  Question: The expression (0 + 1)^* what language does it denotes?
  Answer: {"",(0 + 1),(0 + 1)(0 + 1),(0 + 1)(0 + 1)(0 + 1),...}
  This means ALL strings of 0's and 1's. Can also be indicated by Σ^*
  
  
• Formal languages
  
  A language over Σ is a set of strings of characters drawn from Σ.
  Formal language examples:
  
  Alphabet = English characters
  Language = English sentences
  
  Alphabet = ASCII
  Language = C programs
  
  
• Meaning function (L)
  
  Meaning function L maps syntax to semantics. A meaning function is used:
  • It makes clear what is syntax and what is semantics.
  • Allow us to consider notation as a separate issue.
  • Because expressions and meanings are not 1-1. There are more expressions than meanings. Meaning is many to one and never one to many.
  
  L(e) = M
  e = regular expression
  M = set of strings
  
  Example:
  L(ε) = {""}
  L('c') = {"c"}
  L(A+B) = L(A) ∪ L(B)
  L(AB) = {ab | a∈L(A) ∧ b | b∈L(B)}
  L(A^*) = ∪_i>=0 L(Aⁱ)
  
  
• Regular expression shorthand notation
  • At least one: A⁺ ≡ AA^*
  • Union: A | B ≡ A + B
  • Option: A? ≡ A + ε
  • Range: [a-z] ≡ 'a' + 'b' + 'c' + 'd' + ...
  • Excluded Range: [^a-z] ≡ complement of [a-z]
  
  
• Lexical specifications
  
  Regular expression describe many useful languages.
  Regular languages are a language specification.
  Regular expressions is used as the specification language for lexical analysis.
  
  
  • Keywords
    "if" + "then" + "else"
    
    
  • Integer: a non-empty string of digits
    digit = '0' + '1' + '2' + '3' + '4' + '5' + '6' + '7' + '8'+ '9'
    Integer = digit digit^* = digit⁺
    
    Note:
    * = 0 or more
    + = 1 or more
    
    
  • Identifier: string of letters or digits, starting with a letter
    letter = 'a' + 'b' + 'c' + 'd' + ... + 'A' + 'B' + 'C' + 'D' + ...
    letter = [a-zA-Z]
    Identifier = letter(letter+digit)^*
    
    
  • Whitespace: a non-empty sequence of blanks, newlines and tabs.
    Whitespace = (' ' + '\t' + '\n')⁺
  
  Examples:
  
  Email address = [email protected]
  Email address = letter⁺ '@' letter⁺ '.' letter⁺
  
  number = 12 or 12.34 or 12E+8
  digit = '0' + '1' + '2' + '3' + '4' + '5' + '6' + '7' + '8'+ '9'
  digits = digit⁺
  opt_fraction = ('.'digits) + ε = ('.'digits)?
  opt_exponent = ('E'('+' + '-' + ε) digits) + ε = ('E'('+' + '-')? digits)?
  number = digits opt_fraction opt_exponent
  
  To design the lexical specification of the language the following procedure must be followed:
  
  
  1. Create regular expression for the lexemes of each token class
     • Number = digit⁺
     • Keyword = 'if' + 'else' + ...
     • Identifier = letter(letter+digit)^*
     • OpenPar = '('
     • :
     
     
  2. Construct a gigantic regular expression R, matching all lexemes for all tokens
     
     R = Keyword + Identifier + Number + ...
     R = R₁ + R₂ + R₃ + ...
     
     
  3. Loop thru the input and check it against the meaning function L(R)
     
     Let input be x₁...₂
     For 1 <= i <= n check
         x₁..._i ∈ L(R)
     
     Note:
     
     • Always choose the longest input ("maximal munch").
     • If there is more than one token class which the input might belong choose the one listed first. In the lexical specification, keywords are given a higher priority than identifiers.
     
     
  4. If success then we know that:
         x₁..._i ∈ L(R_j) for some j
     
     If no rule matches, create error strings for all strings not in the lexical specifications.
     Put these error strings last in the priority list.
     
     
  5. Remove x₁..._i from input and go to step 3
  
  
• Finite Automata
  
  Finite automata is used as an implementation model for regular expressions. Regular expressions and finite automaton are very close related. They can specify exactly the same languages called the regular languages.
  
  A finite automaton consists of:
  
  
  • An input alphabet: Σ
  • A finite set of states: S
  • A start state: n
  • A set of accepting states: F ⊆ S
  • A set of transistion states: state ->^input state
  
  The language of a finite automaton ≡ set of strings that the automaton accepts.
  
  
• Deterministic Finite Automata (DFA)
  
  
  • One transistion per input state
  • No ε-moves
  
  A DFA takes only one path through the state graph per input.
  DFAs are faster to execute than NFAs because there are no choices to consider.
  DFAs and NFAs recognize the same set of regular languages.
  
  
• Nondeterministic Finite Automata (NFA)
  
  
  • Can have multiple transistions in a given state
  • Can have ε-moves
  
  An NFA accepts if some choices lead to an accepting state.
  NFAs are, in general, smaller compared to DFAs.
  
  
• Regular expressions into NFAs
  
  Lexical specification we want to implement -> write a set of regular expressions -> translate regex to NFAs -> translate NFAs to DFAs -> implement DFAs as a set of Lookup tables and code for traversing thos tables.
  
  For each kind of regex define an equivalant NFA
  Notation: NFA for regexp M