•  Print this page
    Print this page

Theory of computation
 
 
The theory of computation is mathematically model a machine (for example a computer) and study the theory about it which means what are the problems which would be solved by this machine, what are the limitations of the machine etc.

More information about this subject can be found at: YouTube: Theory of Computation or Automata Theory by Gate Lectures by Ravindrababu Ravula

Ravindrababu Ravula has created more than 70 excellent YouTube movies about this subject.
Based on these YouTube movies, notes have been made which you can find on this page.

Quick guides







Construction of minimal DFA


Information on this page based on: YouTube: Theory Of Computation 2, Construction of minimal DFA and problems

  • Construct a minimal DFA that accepts set of all strings over {a,b} of length 2
    ω ∊ {a,b} and |ω| = 2

    Σ = {a,b}
    L = {aa,ab,ba,bb}

    This DFA is NOT corect. It does accept set of all strings over {a,b} of length 2, but it should also reject strings of other lengths for example: {a,a,a}

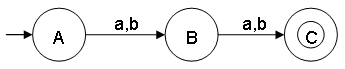
    DFA example 1

    This DFA is corect. It does accept set of all strings over {a,b} of length 2 and rejects strings of other lengths for example: {a,a,a} DFA example 2

    When is the string accepted:
    The string is accepted by the FA if we are able to reach a final state starting from the initial state upon scanning the entire string.

    When is the language accepted:
    The language is accepted by the FA if all strings in the language are accepted.
    All strings not in the language are rejected.

    Notes:
    • A FA can have more than 1 final state.
    • State D is also called the dead or trap state.
    • This minimal DFA has 4 states and state C (also referred as q2) is the final state.
    • The language L is finite which means the FA is finite (= finite number of states).

  • Construct a minimal DFA that accepts set of all strings over {a,b} of length 2 or more
    ω ∊ {a,b} and |ω| >= 2

    L = {aa,ab,ba.bb,aaa, ..., bbb, ...}
    DFA example 3

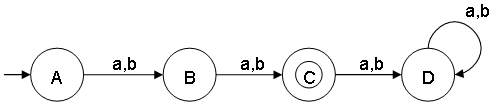
    Notes:
    • For a language L you can draw many DFA diagrams, but there is only 1 minimal DFA.
      The word "minimal" refers to the minimal number of states used.
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • State A represents set of all strings of length 0.
    • State B represents set of all strings of length 1.
    • State C represents set of all strings of length 2.
    • This minimal DFA has 3 states and state C (also referred as q2) is the final state.

  • Construct a minimal DFA that accepts set of all strings over {a,b} of length 2 or less
    ω ∊ {a,b} and |ω| <= 2

    L = {ε,a,b,aa,ab,ba,bb}
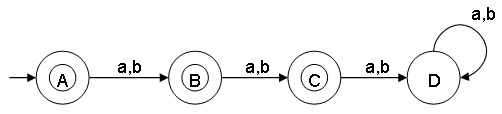
    DFA example 4

    Notes:
    • For a language L you can draw many DFA diagrams, but there is only 1 minimal DFA.
      The word "minimal" refers to the minimal number of states used.
    • The language L is finite which means the FA is finite (= finite number of states).
    • State A represents set of all strings of length 0.
    • State B represents set of all strings of length 1.
    • State C represents set of all strings of length 2.
    • State D represents set of all strings of length 3 or more which will be rejected.
    • If you have ε, always make the inital state a final state.
    • This minimal DFA has 4 states and states A, B and C (respectively referred as q0, q1, q2) are the final states.

  • Number of states required in a minimal DFA that accepts set of all strings with a certain length
    In general a minimal DFA accept strings of length n requiring the following the number of states:

    ω ∊ {a,b}
    |ω| = n, number of states required: (n+2)
    |ω| >= n, number of states required: (n+1)
    |ω| <= n, number of states required: (n+2)

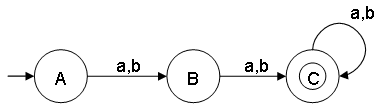
  • Construct a minimal DFA that accepts set of all strings over {a,b}, where the length modulo 2 = 0
    ω ∊ {a,b} and |ω| mod 2 = 0

    L = {ε,aa,ab,ba,bb,aaaa,bbbb,...}

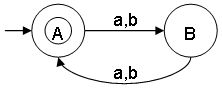
    DFA example 5

    Notes:
    • Even length strings satisfies the condition: |ω| mod 2 = 0
    • ε is a string of length 0 and |ε| mod 2 = 0
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • |ω| mod 2 = 0 can also be written as |ω| ≅ 0 (mod 2). The symbol ≅ means congruent.
    • State A represents set of all strings of even lengths.
    • State B represents set of all strings of odd lengths.
    • This minimal DFA has 2 states and state A (also referred as q0) is the final state.

  • Construct a minimal DFA that accepts set of all strings over {a,b}, where the length modulo 2 = 1
    ω ∊ {a,b} and |ω| mod 2 = 1

    L = {a,b,aaa,aab,...}

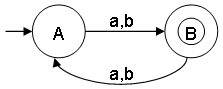
    DFA example 6

    Notes:
    • Odd length strings satisfies the condition: |ω| mod 2 = 1
    • ε is a string of length 0 and does not satisfy condition |ε| mod 2 = 1
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • |ω| mod 2 = 1 can also be written as |ω| ≅ 1 (mod 2). The symbol ≅ means congruent.
    • State A represents set of all strings of even lengths.
    • State B represents set of all strings of odd lengths.
    • This minimal DFA has 2 states and state B (also referred as q1) is the final state.

  • Construct a minimal DFA that accepts set of all strings over {a,b}, where the length modulo 3 = 0
    ω ∊ {a,b} and |ω| mod 3 = 0

    L = {ε,aaa,aab,aaaaaa,...}

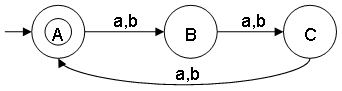
    DFA example 7

    Notes:
    • Strings with lengths 0, 3, 6, 9, ... satisfies the condition: |ω| mod 3 = 0
    • ε is a string of length 0 and does satisfy condition |ε| mod 3 = 0
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • |ω| mod 3 = 0 can also be written as |ω| ≅ 0 (mod 3). The symbol ≅ means congruent.
    • State A represents set of all strings of length 0, 3, 6, 9, ....
    • This minimal DFA has 3 states and state A (also referred as q0) is the final state.

  • Construct a minimal DFA that accepts set of all strings over {a,b}, where the length modulo 3 = 1
    ω ∊ {a,b} and |ω| mod 3 = 1

    L = {a,b,aaaa,aaab,...}

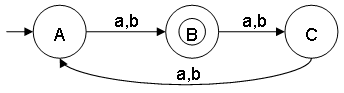
    DFA example 8

    Notes:
    • Strings with lengths 1, 4, 7, 10, ... satisfies the condition: |ω| mod 3 = 1
    • ε is a string of length 0 and does not satisfy condition |ε| mod 3 = 1
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • |ω| mod 3 = 1 can also be written as |ω| ≅ 1 (mod 3). The symbol ≅ means congruent.
    • State B represents set of all strings of length 1, 4, 7, 10, ....
    • This minimal DFA has 3 states and state B (also referred as q1) is the final state.

  • How many states are in a minimal DFA that accepts set of all strings over {a,b}, where the length modulo n = 0
    ω ∊ {a,b} and |ω| mod n = 0

    Answer: The number of states is n

    For example:
    ω ∊ {a,b} and |ω| mod 2 = 0 -> number of states = 2
    ω ∊ {a,b} and |ω| mod 3 = 0 -> number of states = 3
    ω ∊ {a,b} and |ω| mod 4 = 0 -> number of states = 4
    ω ∊ {a,b} and |ω| mod 5 = 0 -> number of states = 5
    ω ∊ {a,b} and |ω| mod 6 = 0 -> number of states = 6
    :

  • Construct a minimal DFA that accepts set of all strings over {a,b}, where the number of "a" are 2
    ω ∊ {a,b} and na(ω) = 2

    L = {aa,baa,aab,aba,aabb,bbaa,bbbaa,...}

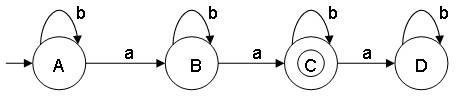
    DFA example 9

    Notes:
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • State A represents set of all strings of length 0
    • State B represents set of all strings of length 1
    • State C represents set of all strings of length 2
    • State D (dead state) represents set of all strings of length 3
    • This minimal DFA has 4 states and state C (also referred as q2) is the final state.

  • Construct a minimal DFA that accepts set of all strings over {a,b}, where the number of "a" are at least 2
    ω ∊ {a,b} and na(ω) >= 2

    L = {aa,aaa,baa,aab,aba,aaab,aabb,bbaa,bbbaa,aaabb,...}

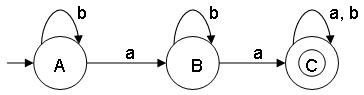
    DFA example 10

    Notes:
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • State A represents set of all strings of length 0
    • State B represents set of all strings of length 1
    • State C represents set of all strings of length 2
    • This minimal DFA has 3 states and state C (also referred as q2) is the final state.

  • Construct a minimal DFA that accepts set of all strings over {a,b}, where the number of "a" is 2 or less
    ω ∊ {a,b} and na(ω) <= 2

    L = {ε,a,b,aa,ab,ba,bb,aab,aba,baa,aabb,aabbb,...}


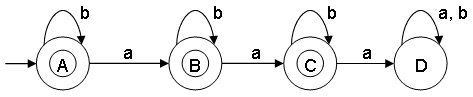
    DFA example 11

    Notes:
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • State A represents set of all strings of length 0
    • State B represents set of all strings of length 1
    • State C represents set of all strings of length 2
    • State D (dead state) represents set of all strings of length 3
    • This minimal DFA has 4 states and state A, B and C (respectively referred as q0, q1 and q2) are the final states.

  • Construct a minimal DFA that accepts set of all strings over {a,b}, where the number of "a" is even
    ω ∊ {a,b} and na(ω) mod 2 = 0

    L = {ε,b,aa,aab,aba,baa,aaaab,aababab,...}


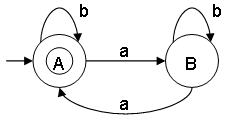
    DFA example 12

    Notes:
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • na(ω) mod 2 = 0 can also be written as na(ω) ≅ 0 (mod 2). The symbol ≅ means congruent.
    • State A represents set of all strings of length 0, 2, 4, 6, 8,... (even lengths)
    • State B represents set of all strings of length 1, 3, 5, 7, 9,... (odd lengths)
    • This minimal DFA has 2 states and state A (also referred as q0) is the final state.

  • Construct a minimal DFA that accepts set of all strings over {a,b}, where the number of "a" is odd
    ω ∊ {a,b} and na(ω) mod 2 = 1

    L = {a,ab,abb,abaa,aaab,aabaaa,ababab,...}


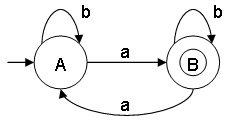
    DFA example 13

    Notes:
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • na(ω) mod 2 = 1 can also be written as na(ω) ≅ 1 (mod 2). The symbol ≅ means congruent.
    • State A represents set of all strings of length 0, 2, 4, 6, 8,... (even lengths)
    • State B represents set of all strings of length 1, 3, 5, 7, 9,... (odd lengths)
    • This minimal DFA has 2 states and state B (also referred as q1) is the final state.

  • Construct a minimal DFA that accepts set of all strings over {a,b}, where the number of "a" modulo 3 = 0
    ω ∊ {a,b} and na(ω) mod 3 = 0

    L = {ε,aaa,aaba,aaab,aaabb,aaaaaa,...}

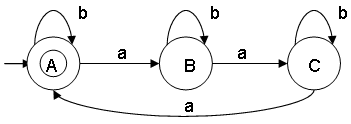
    DFA example 14

    Notes:
    • Strings with lengths 0, 3, 6, 9, ... satisfies the condition: na(ω) mod 3 = 0
    • ε is a string of length 0 and does satisfy condition na(ω) mod 3 = 0
    • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
    • na(ω) mod 3 = 0 can also be written as na(ω) 0 (mod 3). The symbol ≅ means congruent.
    • State A represents set of all strings where the length of "a" are 0, 3, 6, 9, ....
    • This minimal DFA has 3 states and state A (also referred as q0) is the final state.

  • Which state is the final state in a minimal DFA with N states that accepts set of all strings over {a,b}, where the number of "a" modulo N = k
    ω ∊ {a,b} and na(ω) mod N = k and N = number of states

    Answer:

    Number of states = N and ω ∊ {a,b} and na(ω) mod N = k -> final state = qk

    Number of states = N and ω ∊ {a,b} and na(ω) mod N = 0 -> final state = q0
    Number of states = N and ω ∊ {a,b} and na(ω) mod N = 1 -> final state = q1
    Number of states = N and ω ∊ {a,b} and na(ω) mod N = 2 -> final state = q2
    Number of states = N and ω ∊ {a,b} and na(ω) mod N = 3 -> final state = q3
    :

    For example:
    Number of states = 3 and k = 2
    ω ∊ {a,b} and na(ω) mod 3 = 2

    L = {aa,aaaaa,aaaaaaaa,aabb,baaaaa,...}
    Final state = q2

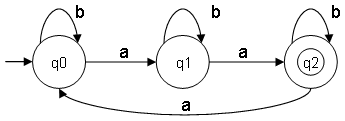
    DFA example 15

    For example:
    Number of states = 4 and k = 1
    ω ∊ {a,b} and na(ω) mod 4 = 1

    L = {a,aaaaa,aaaaaaaaa,ab,aabaaa,...}
    Final state = q1

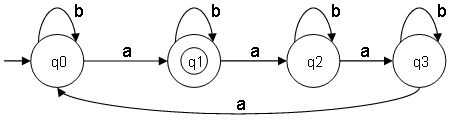
    DFA example 16