Theory of computation

Construction of minimal DFA and cross product of DFA

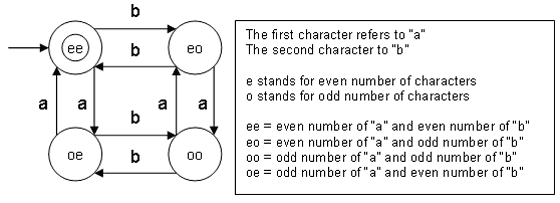
• Construct a minimal DFA that accepts set of all strings over {a,b} in which number of a's and b's are even
  ω ∊ {a,b} and n_a(ω) mod 2 = 0 && n_b(ω) mod 2 = 0
  
  L = {ε,aa,bb,aabb,abab,baba,aaaa,bbbb,...}
  
  
  
  Notes:
  • ε is a string of length 0 and does satisfy condition n_a(ω) mod 2 = 0 and n_b(ω) mod 2 = 0
  • The language L is infinite, we do not know if the FA is finite or infinite. By drawing the FA diagram there are a finite number of states which means this minimal DFA is finite.
  • n_a(ω) mod 2 = 0 can also be written as n_a(ω) 0 (mod 2).
    n_b(ω) mod 2 = 0 can also be written as n_b(ω) 0 (mod 2).
    The symbol ≅ means congruent.
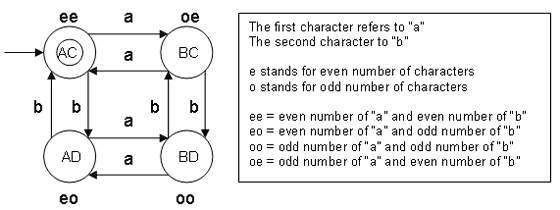
  • The strings are divided in four classes: "ee", "eo", "oe" and "oo".
  • This minimal DFA has 4 states and state "ee" (also referred as q0) is the final state.
  
  
• Construct a minimal DFA that accepts set of all strings over {a,b} in which number of a's and b's are even using cross product
  ω ∊ {a,b} and n_a(ω) mod 2 = 0 && n_b(ω) mod 2 = 0
  
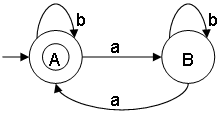
  Counting a's
  
  L = {ε,aa,aaaa,aaaaaa,...}
  
  
  
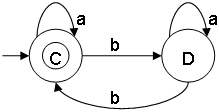
  Counting b's
  
  L = {ε,bb,bbbb,bbbbbb,...}
  
  
  
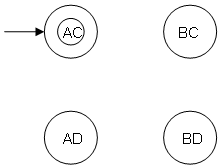
  Cross product (combining a's and b's)
  
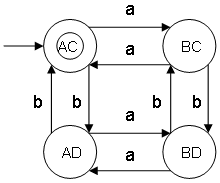
  Multiply the states {A,B} with {C,D}: {A,B} x {C,D} = {AC,AD,BC,BD}
  The cross product consists of 4 states.
  In counting a's, state A is the initial state.
  In counting b's, state C is the initial state.
  AC is the initial state of the 4 states.
  
  
  
  Determine the transition for each state (AC,AD,BC,BD) and for each input (a,b)
  
  
  • State AC and input a
    Counting a's DFA diagram: A -> a -> B
    Counting b's DFA diagram: C -> a -> C
    Result: AC-> a -> BC
    
  • State AC and input b
    Counting a's DFA diagram: A -> b -> A
    Counting b's DFA diagram: C -> b -> D
    Result: AC-> b -> AD
    
  • State BC and input a
    Counting a's DFA diagram: B -> a -> A
    Counting b's DFA diagram: C -> a -> C
    Result: BC-> a -> AC
    
  • State BC and input b
    Counting a's DFA diagram: B -> b -> B
    Counting b's DFA diagram: C -> b -> D
    Result: BC-> b -> BD
    
  • State BD and input a
    Counting a's DFA diagram: B -> a -> A
    Counting b's DFA diagram: D -> a -> D
    Result: BD-> a -> AD
    
  • State BD and input b
    Counting a's DFA diagram: B -> b -> B
    Counting b's DFA diagram: D -> b -> C
    Result: BD-> b -> BC
    
  • State AD and input a
    Counting a's DFA diagram: A -> a -> B
    Counting b's DFA diagram: D -> a -> D
    Result: AD-> a -> BD
    
  • State AD and input b
    Counting a's DFA diagram: A -> b -> A
    Counting b's DFA diagram: D -> b -> C
    Result: AD-> b -> AC
    
  
  
  
  For each state add ee,eo,oe and ee:
  
  
  
  

  a's	logical operator	b's	final states
  e	and	e	{ee}
  e	and	o	{eo}
  o	and	e	{oe}
  o	and	o	{oo}
  e	or	e	{ee,eo,oe}
  e	or	o	{ee,eo,oo}
  o	or	e	{ee,oe,oo}
  o	or	o	{oe,eo,oo}

  
  If counting a's DFA diagram has m number of states and counting b's DFA diagram has n number of states the cross product m x n will have mxn states.