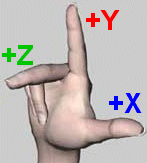Matrix arithmetic and coordinate system.
Information
Coordinate systems
Coordinate systems are used to describe the locations of points in space.
In m3g the orthographic coordinate system is used. In an orthographic coordinate system, the X, Y and Z axis are
perpendicular to each other. The right-hand rule is used, with +Y (index finger) being up,
+X (thumb) horizontal to the right, and +Z (middle) directed toward the viewer.
All angles or rotational representations are in degrees. A positive rotation is
counter clockwise.
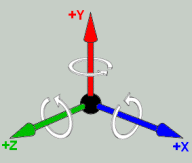
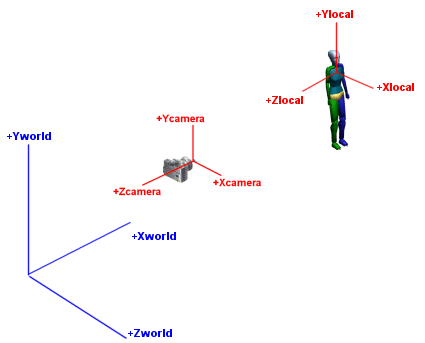
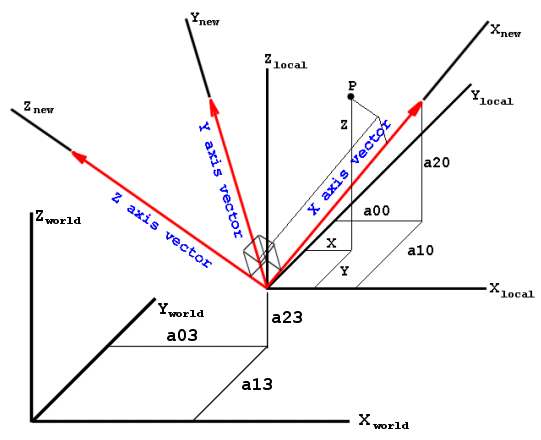
In m3g, three coordinate systems plays an important role:
- World coordinate system.
Is the base on which all other coordinates are being defined.
- Camera coordinate system.
This coordinate system is aligned with the eye or camera.
The
+Y axis is up, and the -Z axis points out off the camera.
In order to render the world, everything in the scene must be transformed to camera
coordinates.
- Local (or object) coordinate system.
Each object in the scene is defined in its own local coordinate system.
By using a local coordinate system you can create many copies of the object,
in different positions and orientations.
Matrix arithmetic
A 3x3 matrix can be used to represent a scaling [S] (resize an object) or
rotation [R] (rotate an object about the origin by an angle Θ).
A 3x1 matrix can be used to represent a translation [T] (moves an object).
A 4x4 matrix can be used to combine a scaling or rotation with a translation.
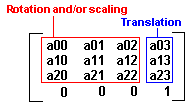
The meaning of values a00...a23 are explained in the figures below:


A 4x4 matrix can store a single transformation (= rotation, scaling or translation) or a sequence of transformations.
The latter is called a composite transformation. The matrix of a composite transformation
is obtained by multiplying the matrices of the individual transformations.
The order of multiplying the matrices matters.
Composite transformations are built from left to right.
The product [S][R][T] (in that order) is the matrix of the composite transformation that
first scales, then rotates, then translates.
The matrix produced by the product [S][R][T] is different from the matrix produced by
the product [T][R][S].
Rotations around the XYZ axes are necessary in order to
describe any orientation of a body in space.
Rotations about each axis are often used to transform between different coordinate systems.
By using multiple coordinate systems, graphics algorithms are made easier to understand and to implement.
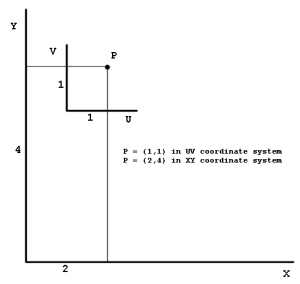
In the figure below the two coordinate systems represent point P (in 2D space) in different ways.
The three rotation matrices are given below:
Rotation tx around the X-axis:
 |
|
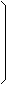 |
= |
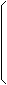 |
| 1 |
0 |
0 |
| 0 |
cos(tx) |
sin(tx) |
| 0 |
-sin(tx) |
cos(tx) |
|
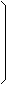 |
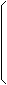 |
|
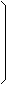 |
Rotation ty around the Y-axis:
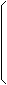 |
|
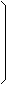 |
= |
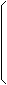 |
| cos(ty) |
0 |
-sin(ty) |
| 0 |
1 |
0 |
| sin(ty) |
0 |
cos(ty) |
|
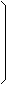 |
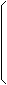 |
|
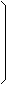 |
Rotation tz around the Z-axis:
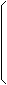 |
|
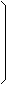 |
= |
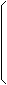 |
| cos(tz) |
sin(tz) |
0 |
| -sin(tz) |
cos(tz) |
0 |
| 0 |
0 |
1 |
|
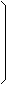 |
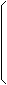 |
|
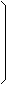 |
In games development, the particular order of rotations is to rotate about the Y-axis first, then the X-axis,
then the Z-axis:
Rz(t) Rx(t) Ry(t) combined in a single matrix is:
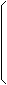 |
|
cos(tz) cos(ty) +
sin(tz) sin(tx) sin(ty)
|
sin(tz) cos(tx)
|
-cos(tz) sin(ty) +
sin(tz) sin(tx) cos(ty)
|
|
-sin(tz) cos(ty) +
cos(tz) sin(tx) sin(ty)
|
cos (tz) cos(tx)
|
sin(tz) sin(ty) +
cos(tz) sin(tx) cos(ty)
|
|
cos(tx) sin(ty)
|
-sin(tx)
|
cos(tx) cos(ty)
|
|
 |
Rotation and translation about or in a particular axis are also indicated by a name:
- Pitch :Rotation about X-axis
- Yaw :Rotation about Y-axis
- Roll :Rotation about Z-axis
- Strafe :Translation in X-axis
- Fly :Translation in Y-axis
- Move :Translation in Z-axis
|