This tool calculates how much interest is added to the initial principal amount, so that, from that moment on, the interest that has been added
also earns interest. This addition of interest to the principal is called compounding.
It can be calculated using the following equation:
FV = P * (1 + (R / N))N * T or FV = P + I
where:
FV = Future value
I = Interest amount
P = Principal initial amount
R = Nominal interest rate per year (as a decimal, not in percentage)
T = Time period in years
N = Number of compounding periods in one year
Example:
John deposit $1000 in a bank account offering 3.5% interest, compounded quarterly.
Question:
After 2 years how much money will John earn?
Future value FV = 1000 * (1 + (0.035 / 4))4 * 2 = $1072.18
Interest amount I = 1072.18 - 1000 = $72.18
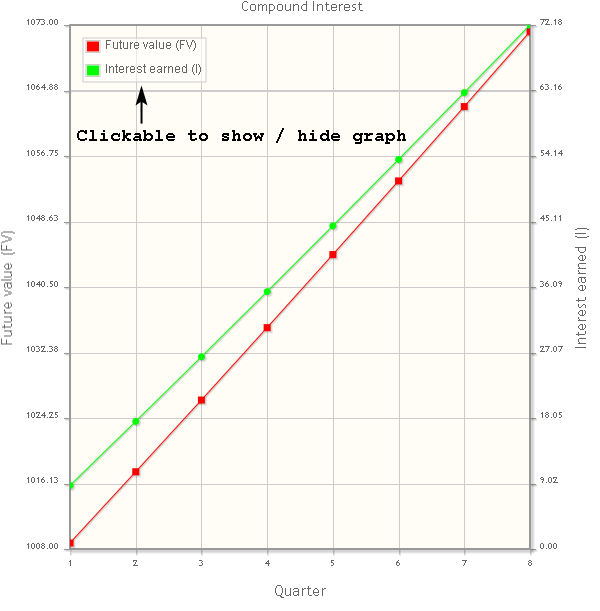
This tools also calculates the interest (I) and future value (FV) for each componding period and plot these data into a single graph, for example:
======================================================
Quarter Interest earned (I) Future value (FV)
======================================================
1 8.75 1008.75
2 17.58 1017.58
3 26.48 1026.48
4 35.46 1035.46
5 44.52 1044.52
6 53.66 1053.66
7 62.88 1062.88
8 72.18 1072.18
This compound interest calculator has many features:

- Calculate the future value (FV) using equation:
FV = P * (1 + (R / N))N * T
- Calculate the principal initial amount (P) using equation:
|
P =
|
FV
|
or
|
P =
|
I
|
|
(1 + (R / N))N * T
|
(1 + (R / N))N * T - 1
|

- Calculate the nominal interest rate (R) per year (as a decimal, not in percentage) using equation:
R = N * ((FV / P)1 / (N * T) - 1)
or
R = N * ((I / P) + 1)1 / (N * T) - 1)
- Calculate the time period (T) in years using equation:
|
T =
|
log(FV / P)
|
or
|
T =
|
log((I / P) + 1)
|
|
N * log(1 + (R / N))
|
N * log(1 + (R / N))
|

- Calculate the compounding periods (N) in one year using equation:
|
N =
|
log(FV / P)
|
or
|
N =
|
log((I / P) + 1)
|
|
T * log(1 + R)
|
T * log(1 + R)
|

- Calculate the effective interest rate (Re) per year (as a decimal, not in percentage) using equation:
Re = (1 + (R / N))N - 1
Note:
The effective interest rate is the equivalent rate of compound interest earned over a period of one year
for a nominal interest rate per year which is compounded twice or more over the year.
- Let you specify the compounding period:
- daily
360, 364, 365 or 366 times per year
- weekly
52 times per year
- bi-weekly (every two weeks)
26 times per year
- semi-monthly (twice a month)
24 times per year
- monthly
12 times per year
- bi-monthly (every two months)
6 times per year
- quarterly
4 times per year
- semi-annually (twice a year)
2 times per year
- yearly
1 time per year
- Let you specify the time period in two ways:
- Method 1: Enter the time period by number of: days, weeks, bi-weeklies, semi-monthlies, months, bi-monthlies, quarters, semi-annuallies or years.
- Method 2: Enter a from date and to date. Both dates can also be included or excluded.
- Set the number of days in a year to 360, 364, 365 or 366 days.
- Draw two graphs in a single plot (see image above).
- Graph 1: Compound period (N) - Future value (FV)
- Graph 2: Compound period (N) - Interest earned (I)
To show/hide a graph click on "Future value (FV)" or "Interest earned (I)" in the plot legend.
Press button "Make plot image" to create an image which can be saved.
Input compound interest calculator with graph:
|
|